Cтруктуры данных
Что такое структуры данных?
Структура данных – это контейнер, который хранит информацию в определенном виде.
Из-за такой «компоновки» она может быть эффективной в одних операциях и неэффективной в других. Цель разработчика – выбрать из существующих структур оптимальный для конкретной задачи вариант.
Зачем нужны структуры данных?
Данные являются самой важной сущностью в информатике, а структуры позволяют хранить их в организованной форме.
В зависимости от ситуации данные должны храниться в некотором определенном формате. Структуры данных предлагают несколько вариантов таких размещений.
8 часто используемых структур
Часто используемые структуры данных:
- Массив (Array)
- Стек (Stack)
- Очередь (Queue)
- Связный список (Linked List)
- Дерево (Tree)
- Граф (Graph)
- Префиксное дерево (Trie)
- Хэш-Таблица (Hash Table)
Массивы
Массив – это самая простая и наиболее широко используемая из структур. Стеки и очереди являются производными от массивов. Вот изображение простого массива размером 4, содержащего элементы (1, 2, 3 и 4).
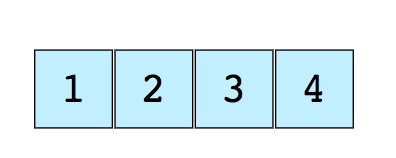
Каждому из них присваивается неотрицательное числовое значение – индекс, который соответствует позиции этого элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Существует два типа массивов:
- Одномерные массивы (как на картинке).
- Многомерные массивы (массивы массивов).
Основные операции с массивами
- Insert – вставка.
- Get – получение элемента.
- Delete – удаление.
- Size – получение общего количества элементов в массиве.
Частые вопросы о массивах
- Найти второй минимальный элемент.
- Первые не повторяющиеся целые числа.
- Объединить два отсортированных массива.
- Переставить положительные и отрицательные значения.
Стеки
Пример стека из реальной жизни – куча книг, лежащих друг на друге. Чтобы получить книгу, которая находится где-то в середине, вам нужно удалить все, что лежит сверху. Так работает метод LIFO (Last In First Out, последним пришел – первым ушел).
Вот изображение стека, содержащего три элемента (1, 2 и 3). Элемент 3 находится сверху и будет удален первым:
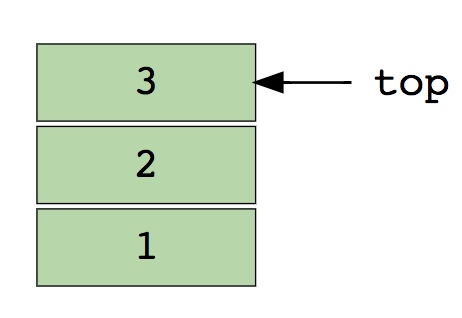
Основные операции со стеками
- Push – вставка элемента наверх стека.
- Pop – получение верхнего элемента и его удаление.
- isEmpty – возвращает true, если стек пуст.
- Top – получение верхнего элемента без удаления.
Часто задаваемые вопросы о стеках
- Вычисление постфиксного выражения с помощью стека.
- Сортировка значений в стеке.
- Проверка сбалансированности скобок в выражении.
Очереди
Как и стек, очередь – это линейная структура данных, которая хранит элементы последовательно. Единственное существенное различие заключается в том, что вместо использования метода LIFO, очередь реализует метод FIFO (First in First Out, первым пришел – первым ушел).
Идеальный пример этих структур в реальной жизни – очереди людей в билетную кассу. Если придет новый человек, он присоединится к линии с конца, а не с начала. А человек, стоящий впереди, первым получит билет и, следовательно, покинет очередь.
Вот изображение очереди, содержащей четыре элемента (1, 2, 3 и 4). Здесь 1 находится вверху и будет удален первым:
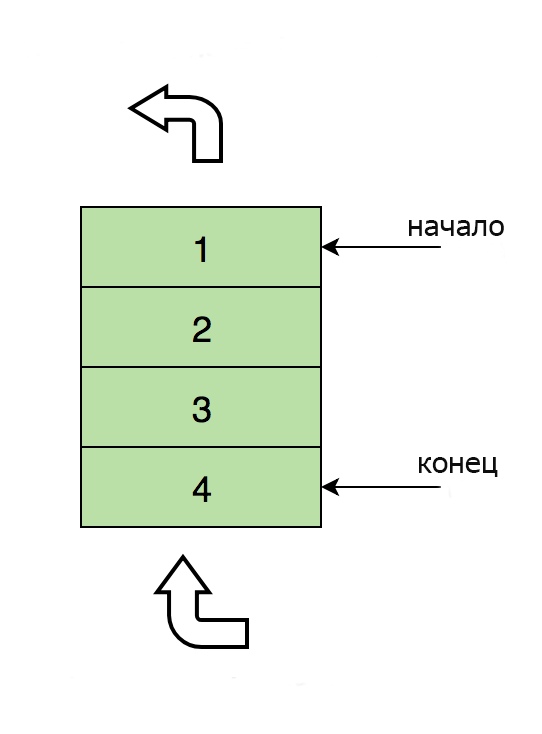
Основные операции с очередями
- Enqueue – вставка в конец.
- Dequeue – удаление из начала.
- isEmpty – возвращает true, если очередь пуста.
- Top – получение первого элемента.
Часто задаваемые вопросы об очередях
- Реализация стека с помощью очереди.
- Развернуть первые k элементов.
- Генерация двоичных чисел от 1 до n с помощью очереди.
Связный список
Еще одна важная линейная структура данных, которая на первый взгляд похожа на массив, но отличается распределением памяти, внутренней организацией и способом выполнения основных операций вставки и удаления.
Связный список – это сеть узлов, каждый из которых содержит данные и указатель на следующий узел в цепочке. Также есть указатель на первый элемент – head. Если список пуст, то он указывает на null.
Связные списки используются для реализации файловых систем, хэш-таблиц и списков смежности.
Вот визуальное представление внутренней структуры связного списка:

Типы связных списков:
- Однонаправленный
- Двунаправленный
Основные операции со связными списками
- InsertAtEnd – вставка в конец.
- InsertAtHead – вставка в начало.
- Delete – удаление указанного элемента.
- DeleteAtHead – удаление первого элемента.
- Search – получение указанного элемента.
- isEmpty – возвращает true, если связный список пуст.
Часто задаваемые вопросы о связных списках
- Разворот связного списка.
- Обнаружение цикла.
- Получение N-го узла с конца.
- Удаление дубликатов.
Графы
Граф представляет собой набор узлов, соединенных друг с другом в виде сети. Узлы также называются вершинами. Пара (x, y) называется ребром, которое указывает, что вершина xсоединена с вершиной y. Ребро может содержать вес/стоимость, показывая, сколько затрат требуется, чтобы пройти от x до y.
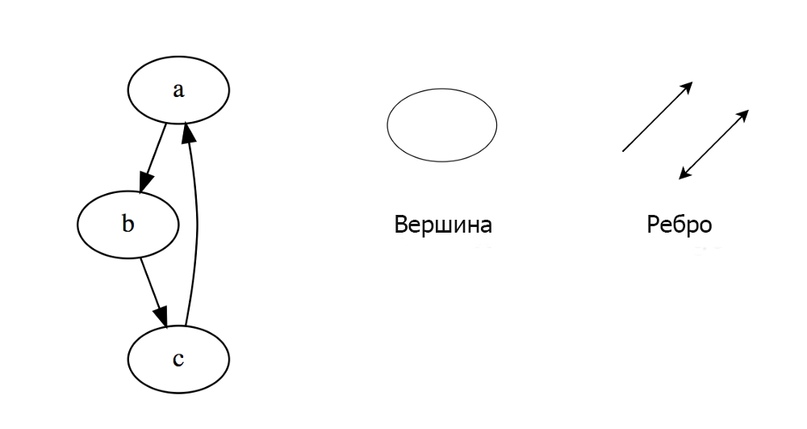
Типы графов:
- Неориентированный
- Ориентированный
В языке программирования графы могут быть представлены в двух формах:
- Матрица смежности
- Список смежности
Общие алгоритмы обхода графов:
- В ширину
- В глубину
Часто задаваемые вопросы о графах
- Реализовать поиск по ширине и глубине.
- Проверка, является ли граф деревом.
- Количество ребер в графе.
- Кратчайший путь между двумя вершинами.
Деревья
Дерево – это иерархическая структура данных, состоящая из вершин (узлов) и ребер, соединяющих их. Они похожи на графы, но есть одно важное отличие: в дереве не может быть цикла.
Деревья широко используются в искусственном интеллекте и сложных алгоритмах для обеспечения эффективного механизма хранения данных.
Вот изображение простого дерева, и основные термины:
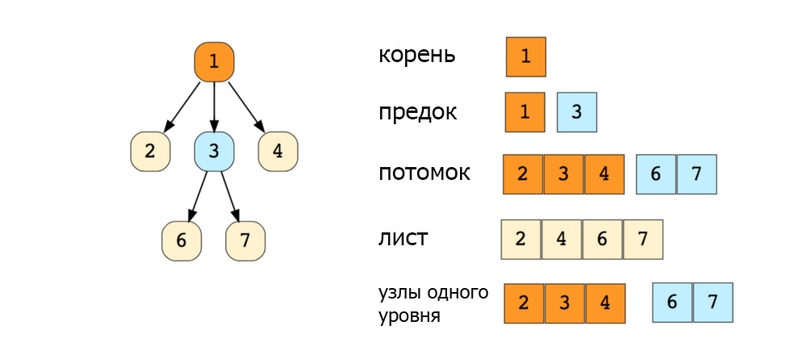
Типы деревьев:
- N-арное дерево;
- сбалансированное дерево;
- бинарное дерево;
- бинарное дерево поиска;
- дерево AVL;
- красно-чёрное дерево;
- 2-3 дерево.
Из всех типов чаще всего используются бинарное дерево и бинарное дерево поиска.
Часто задаваемые вопросы о деревьях
- Высота бинарного дерева.
- Найти k-ое максимальное значение в дереве бинарного поиска.
- Узлы на расстоянии k от корня.
- Предки заданного узла в бинарном дереве.
Префиксное дерево
Префиксные деревья (tries) – древовидные структуры данных, эффективные для решения задач со строками. Они обеспечивают быстрый поиск и используются преимущественно для поиска слов в словаре, автодополнения в поисковых системах и даже для IP-маршрутизации.
Вот иллюстрация того, как три слова top, thus и their хранятся в префиксном дереве:
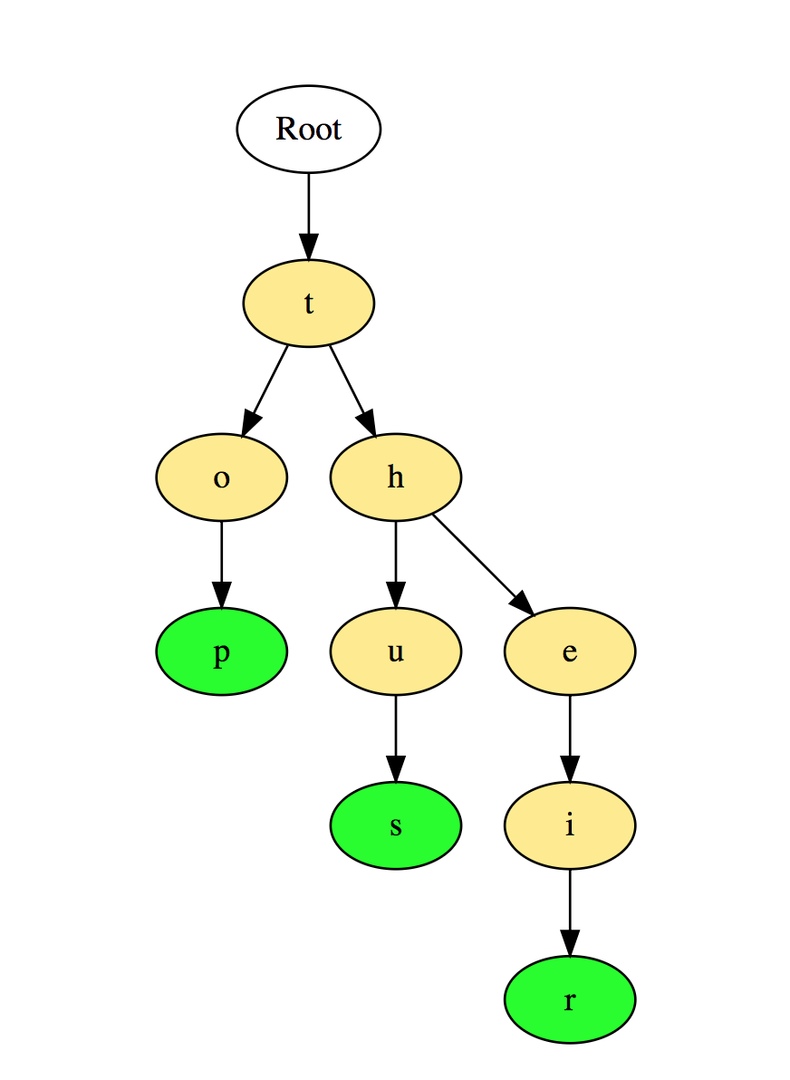
Слова размещаются сверху вниз. Выделенные зеленым элементы показывают конец каждого слова.
Часто задаваемые вопросы о префиксных деревьях
- Общее количество слов.
- Вывод всех слов.
- Сортировка элементов массива.
- Формирование слов из словаря.
- Создание словаря T9.
Хеш-Таблица
Хеширование – это процесс, используемый для уникальной идентификации объектов и хранения каждого из них в некотором предварительно вычисленном уникальном индексе – ключе. Итак, объект хранится в виде пары ключ-значение, а коллекция таких элементов называется словарем. Каждый объект можно найти с помощью его ключа. Существует несколько структур, основанных на хешировании, но наиболее часто используется хеш-таблица, которая обычно реализуется с помощью массивов.
Производительность структуры зависит от трех факторов:
- функция хеширования;
- размер хеш-таблицы;
- метод обработки коллизий.
Вот иллюстрация того, как хэш отображается в массиве. Индекс вычисляется с помощью хеш-функции.
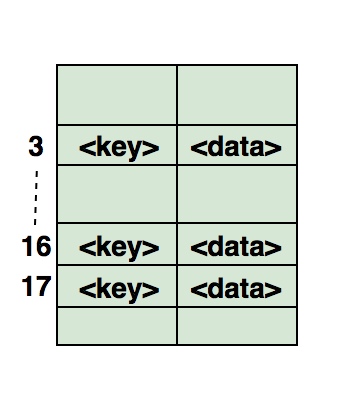
- Часто задаваемые вопросы о хеш-таблицах
- Найти симметричные пары.
- Определить, является ли массив подмножеством другого массива.
- Проверить, являются ли массивы непересекающимися.
Перевод статьи Fahim ul Haq: The top data structures you should know for your next coding interview